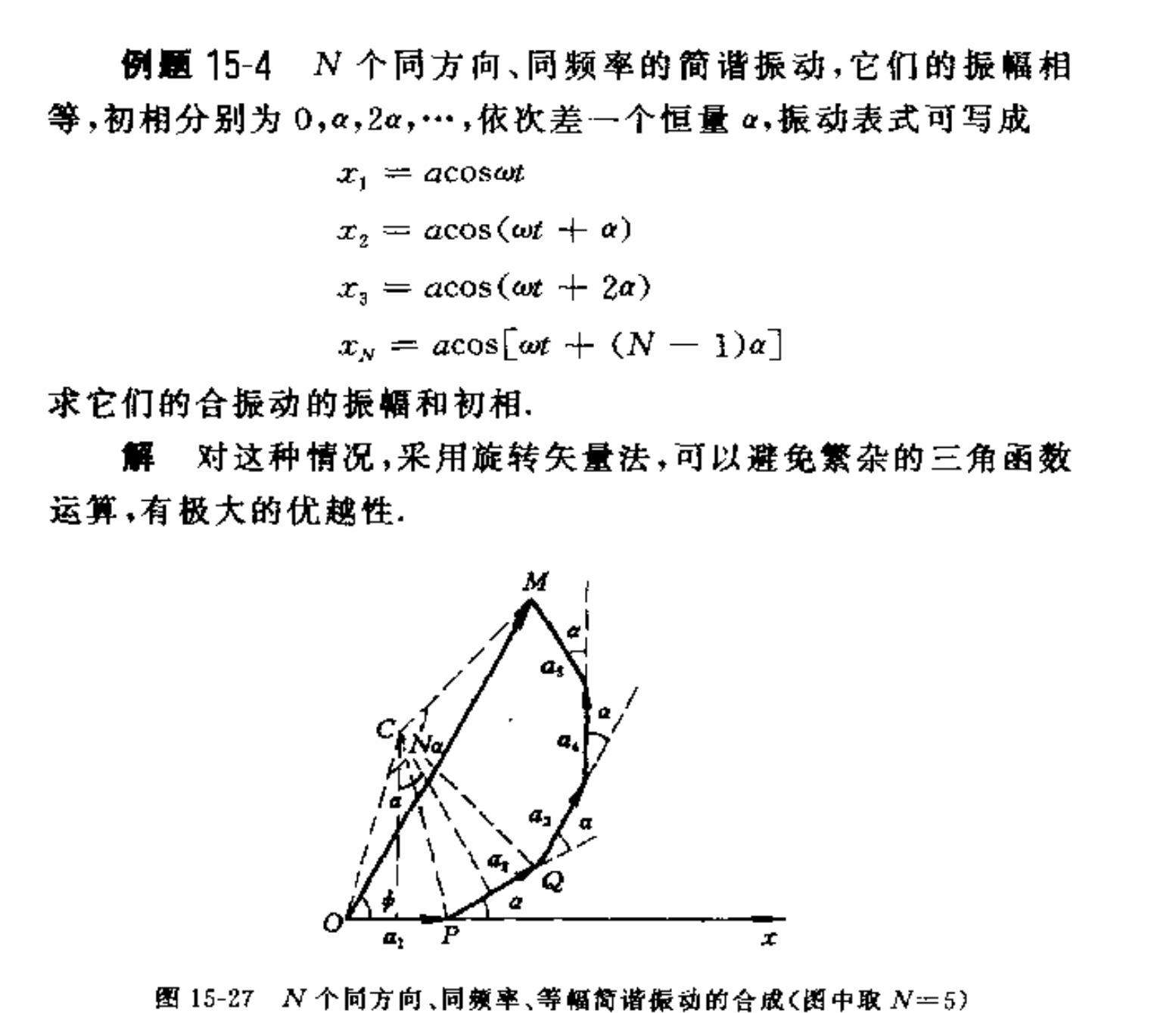
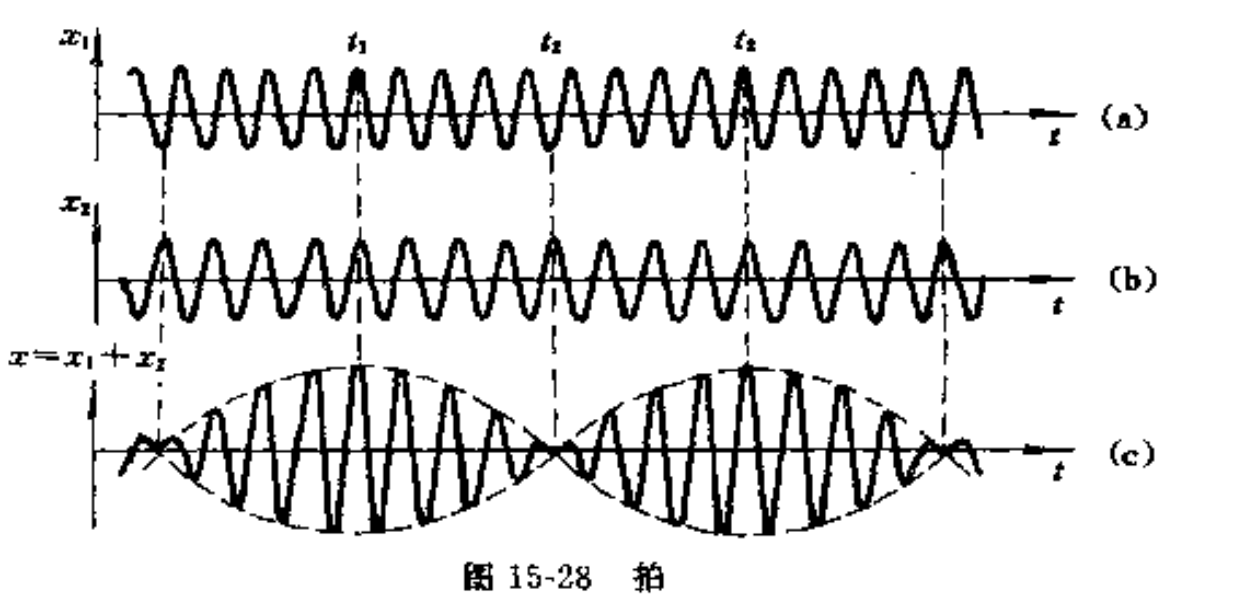
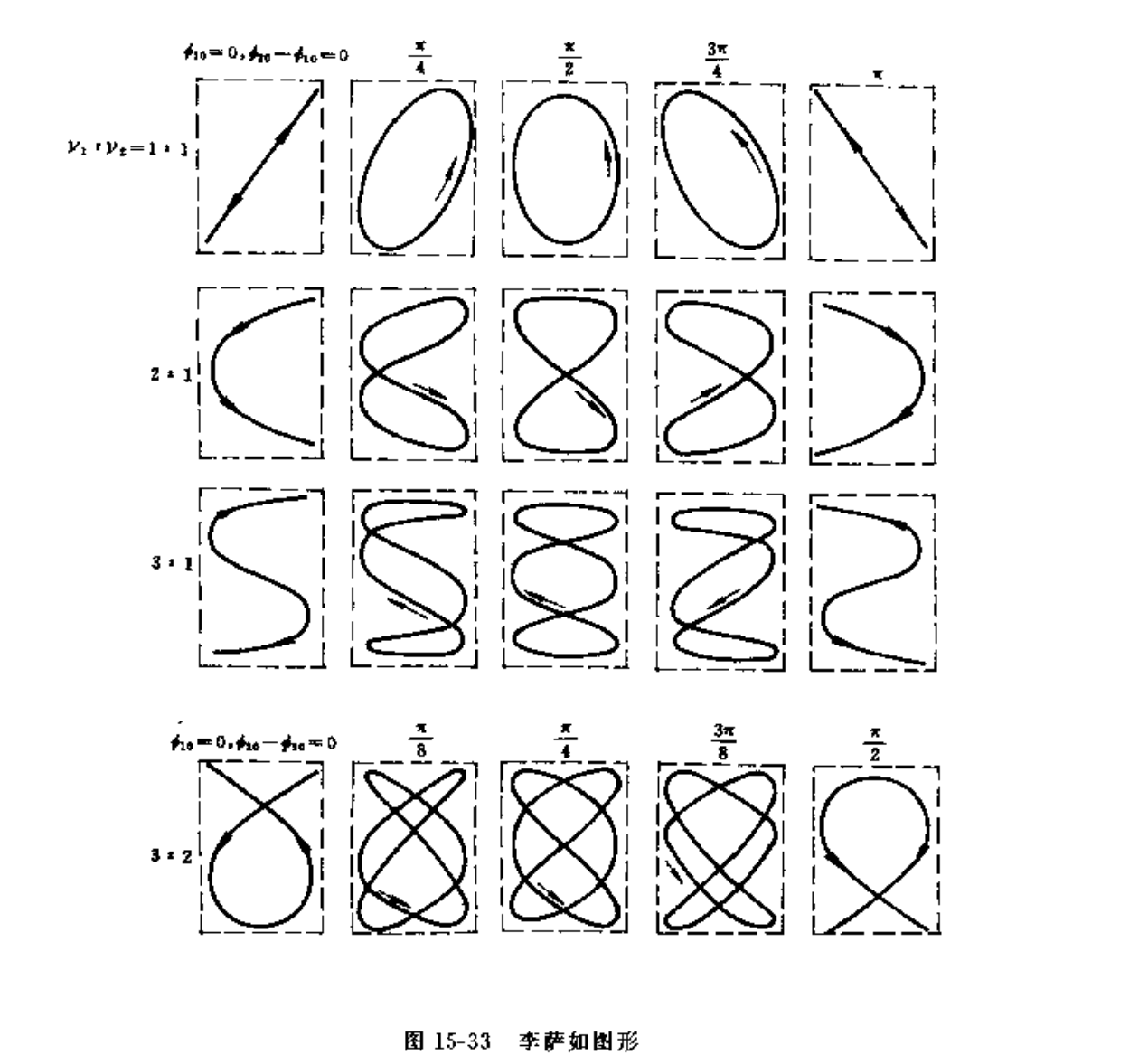
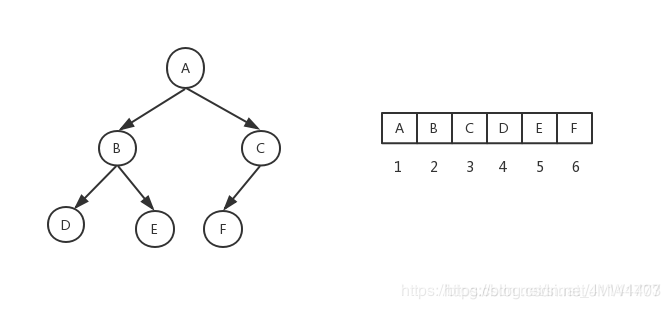
锁存器

SR锁存器

SR锁存器的两种组成方式

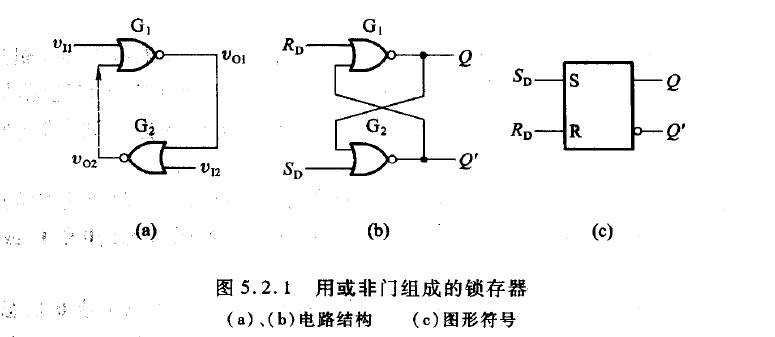
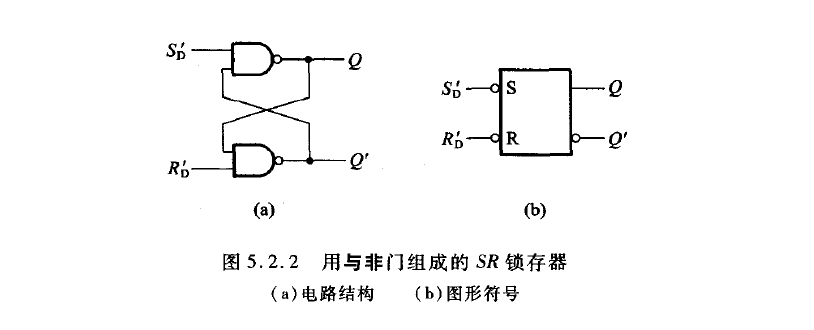
无论是哪一种SR锁存器，其底层逻辑都是一致的，可以用以下几句话概括：

1. 或非门SR锁存器是正逻辑，与非门SR锁存器是反逻辑。
2. 当S=R=0时，锁存器输出保持上一个时刻的输出。（对于反逻辑而言。即S’=R’=1）
3. 当S=1，R=0时，进入Set模式，输出端置1。
4. 当S=0，R=1时，进入Reset模式，输出端置0。
5. 当S=R=1时，分以下两种情况：
   a. 对于正逻辑锁存器，均输出0
   b. 对于反逻辑锁存器，均输出1
   这种情况下，当S，D的信号同时变为0后状态不定。

由此可知，对于正常的情况，我们应当保证S·R=0的约束条件。但是要注意理解，当情况5中下一时刻S与R错开变化，我们其实是可以预测下一时刻电路的输出状态的。
下面是正逻辑SR锁存器的真值表

下面是反逻辑SR锁存器的真值表

注意这两种触发器真值表的最后两行不是一样的！另外这个电路要自己画一遍。

触发器

电平触发

电平触发的SR触发器

当触发信号CLK变成高电平后，SR锁存器才正常工作，否则SR锁存器将保持原有输出，无论S与R的输入情况如何。具有这种性质的触发器就是电平触发器。
这种触发器的操作效果可以这样表述：

1. CLK=0，电路保持原状态输出
2. CLK=1，电路变成SR锁存器电路。
   电平触发的触发器有这样的作用特点：
3. 只有当CLK有效的时候才需要看输入情况.
4. 在CLK=1的全部时间里，SR的状态都会引起输出变化；CLK回到0后，触发器保存着前一瞬间的状态。
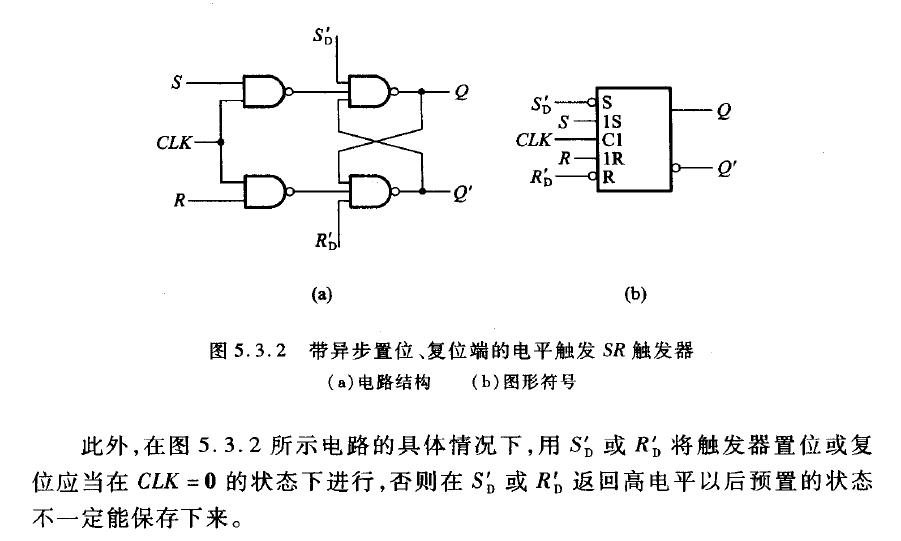
   下面介绍带异步置位复位端口的电平触发SR触发器。
   他的思路也很简单：在原有的电平触发SR触发器的基础上，添加两个优先级更高的信号S’,R’，若这两个信号有效，只要相应地将其置为1或0即可；当这两个信号无效，则进入一般的电平触发SR触发器
   下面给出SR触发器的逻辑图：
   
   
   在CLK=1时，同步SR触发器的真值表与一般SR触发器完全相同；在CLK=0时，电路出于保持状态。
   相关真值表此处从略

电平触发的D触发器

D触发器的发明是为了先天地去除可能使得SR触发器中S=R=1的情况的一种设计，它其实就是把
将SR触发器中的输入端利用同一个信号D及其反信号作为输入信号D’作为S和R端输出，得到的就是电平触发的D触发器。
其逻辑图如下：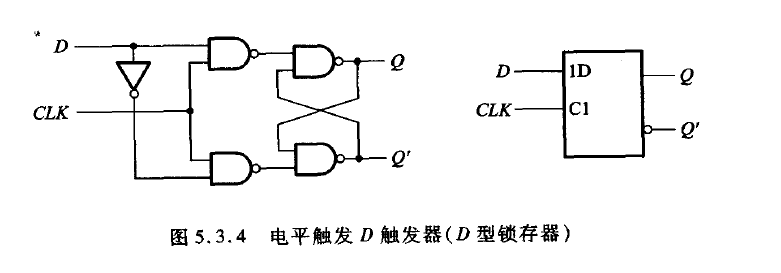

由此可见，这样的方式先天避免了S=R=1的可能性，但是也使得S=R=0变得不可能。为了使电路保持功能完整，我们规定：
CLK定好为低电平时，为D型锁存器的保持态。

边沿触发

我们直接来看一个例子：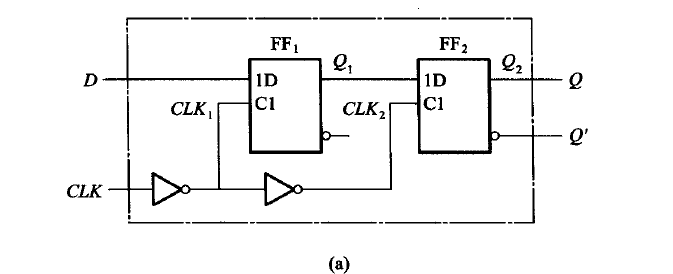

分析以下CLK从0->1(上升沿)的电路变化：
CLK=0时：

1. CLK=0，CLK1=1，CLK2=0
2. FF1有效，FF2无效
3. Q1随着输入信号D同步变化，即Q1=D
4. Q=Q2不变（注意，此前我一直以为这是会变化的！）

CLK=1时：

1. CLK=1，CLK1=0，CLK2=1
2. FF2有效，FF1无效
3. Q1=D不再变化
4. Q2=Q1=D

由此我们可以知道，这种上升沿边沿触发器有以下特点：

1. 触发器的次态输出仅仅取决于上升沿到达前瞬间输入的逻辑状态，在一个时钟周期内上升沿到来前后，输入信号的变化对触发器的次态没有影响
2. 从结果上看，以上升沿边沿触发器为例，输出信号只有在CLK信号上升沿到来处才有可能发生变化（分析波形图的时候可以直接判断这些关键节点）

至于下降沿边沿触发其的特点则可以完全对称地总结下来，这里从略。
下面看一下边沿触发方式的判断方法：

1. 前非后不非->上升沿（符号不带圈）
2. 后非前不非->下降沿（符号带圈）

   脉冲触发

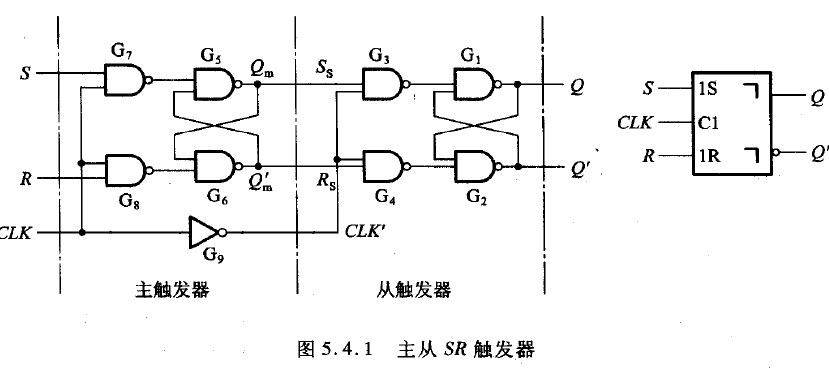
   主从SR触发器（MSSR触发器）

   
   我们来尝试分析以下这个电路：
3. CLK=0，CLK’=1,主触发器FF1，从触发器FF2均出于保持态。（虽然FF2的时钟信号是有效的，由于前一级的信号不会变，所以这一级的信号也不变，体现“主从”关系）
4. CLK->1，上升沿到来时，Qm随着S和R的变化而变化，而从触发器保持原来的状态不变。
5. CLK->0，下降沿到来时，从触发器的输出Q被置为此刻Qm的相同状态。

简单来说就是：

1. 在一个时钟周期里只有CLK下降沿处（或上升沿，取决于电路结构）可能会发生输出端状态的改变。
2. 在脉冲触发中，不能仅仅根据CLK下降沿（或上升沿）到来的前一时刻的输入状态来确定输出端的状态，必须要考虑CLK=1（或0，表示边沿到来前）主触发器的变化。

JK触发器

先来看下这个令人遐想连篇（雾）的触发器的逻辑图，以及教材上对她的解读：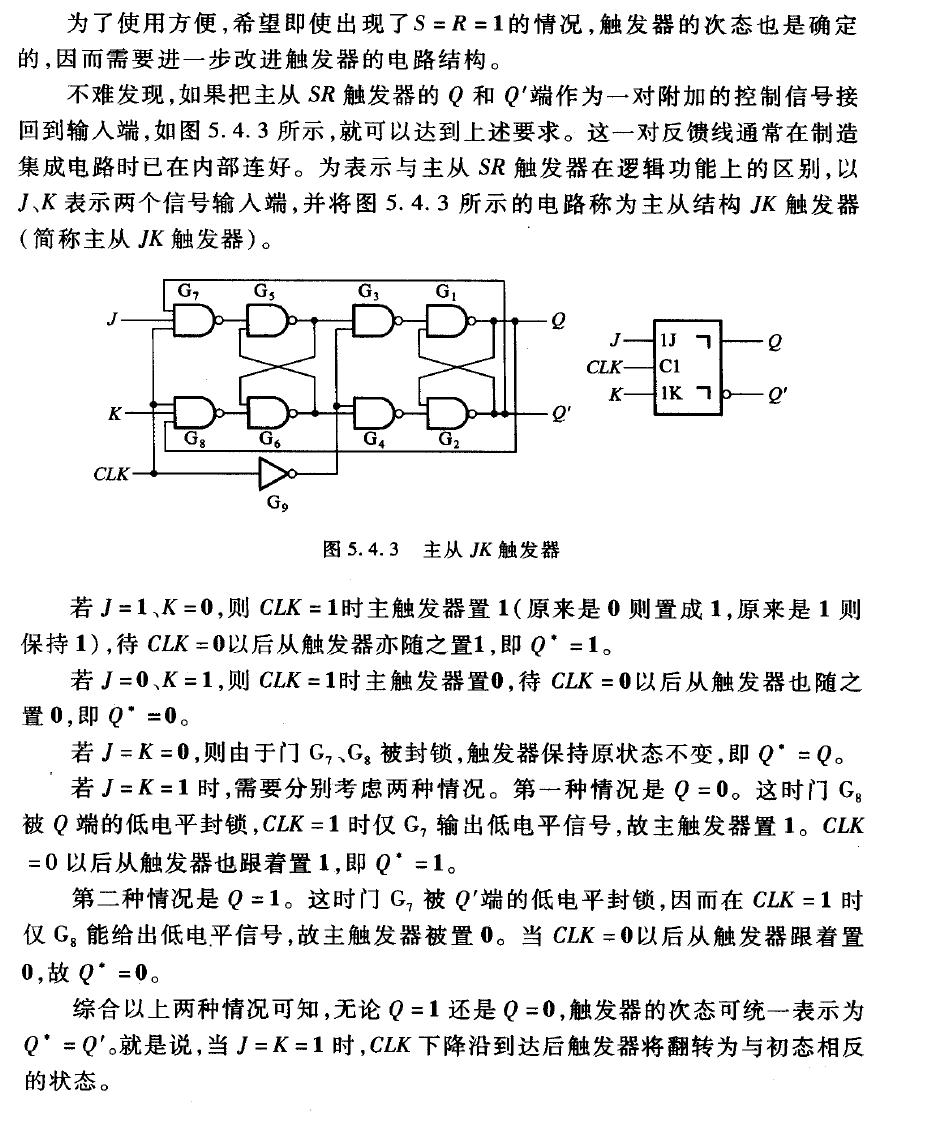

简单来说，JK触发器的逻辑功能就是：

1. CLK下降沿（或上升沿）触发
2. 触发时，J=S，K=R
3. 唯一的区别：J=R=1时，确定次态变为当前态的反态

按逻辑功能分类的触发器

触发器的逻辑表达式：

1. SR触发器： $$Q^*=S'R'Q+SR'Q'+SR'Q=S+R'Q\\SR=0$$
2. JK触发器： $$Q^*=JQ'+K'Q$$
3. T触发器： $$Q^*=TQ'+T'Q=T异或Q$$
4. D触发器： $$Q^*=D$$

我们做的问题是：第十六届华中杯问题C。这个问题在数学建模竞赛中属于十分简单的问题。我大体的思路就是：

问题一思路：

1. 归一化波长数据
2. 画出归一化波长-横坐标散点图
3. 得到散点图后，判断适合用何种曲线拟合
4. 采用数据点拟合并画图
5. 选择合适的插值方法，插入数据点后再次拟合
6. 比较两次拟合的结果

问题二思路：

1. 采用迭代方法求函数的离散表达式（可取x区间长0.01等）
2. 增加迭代次数，更改迭代模型（几何近似or微分）
3. 建立曲线函数表达式，分析不同情况下求得函数表达式的精确性

问题三思路：

1. 采用问题二的最佳方案，划分训练集和测试集
2. 利用训练集求出预测函数表达式，再对测试集进行预测
3. 对结果进行误差分析（残差，均方误差），分析误差产生的原因

此后，我阅读了某优秀论文，发现其基本思想与我几乎一致。

对于我们初学者想到的这种老套的既有模型，我的总结如下：

1. 本次第一题的结果几乎都维持在2.2附近，这说明曲线的曲率近似为定值，应想到原曲线为一个圆。这说明我们对结果的解释不够完善。在做完一件事之后，一定要回头给一个好的解释。
2. 不应该拘泥于题目文件本身，积极寻找相关领域论文，从机理方面做误差分析等实际情况的考虑。
3. 公式过程十分完善，推导很“数学”。虽然使用的都是可以用既有Matlab或Python函数求解的模型，但数模究竟是数模，必须要有完善的数学推理，这部分要把b装足了。
4. 学会变着法儿画图，但是要对每个图片的意义做好阐述。不要认为联系实际，给出合理解释的部分比较low！
5. 有时候，我们只能想到一个大致的思路，但是可以由此触发比较高级的算法，例如想到要插值，可以选用不太老套的插值方法。
6. 不要小看中学数学中学过的初等几何知识。

定位为编程辅助建模，意味着二者我都要会！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

# 原始数据
test_1 = np.array([1529.808, 1529.807, 1529.813, 1529.812, 1529.814, 1529.809])
test_2 = np.array([1541.095, 1541.092, 1541.090, 1541.093, 1541.094, 1541.091])

# 归一化 (标准化可选)
test1 = test_1 / np.mean(test_1)
test2 = test_2 / np.mean(test_2)
dist = 0.6

# 生成测试点位置
test_points = np.array([1*dist, 2*dist, 3*dist, 4*dist, 5*dist, 6*dist])

# 构建 DataFrame
df = pd.DataFrame({
    "testpoint": test_points,
    "test1": test1,
    "test2": test2
})

# 提取数据
x = df["testpoint"].values
y1 = df["test1"].values
y2 = df["test2"].values

# 三次多项式拟合
coef1_cubic = np.polyfit(x, y1, 3)
coef2_cubic = np.polyfit(x, y2, 3)
poly1_cubic = np.poly1d(coef1_cubic)
poly2_cubic = np.poly1d(coef2_cubic)

# 生成更平滑的拟合曲线
x_dense = np.linspace(min(x), max(x), 100)
y1_dense = poly1_cubic(x_dense)
y2_dense = poly2_cubic(x_dense)

# 绘图
plt.figure(figsize=(8, 5))
plt.scatter(x, y1, color="blue", label="Test1 Data")
plt.scatter(x, y2, color="red", label="Test2 Data")
plt.plot(x_dense, y1_dense, linestyle="--", color="blue", alpha=0.7, label="Cubic Fit 1 (smooth)")
plt.plot(x_dense, y2_dense, linestyle="--", color="red", alpha=0.7, label="Cubic Fit 2 (smooth)")

plt.xlabel("Test Point Distance")
plt.ylabel("Normalized Wavelength")
plt.legend()
plt.title("Cubic Polynomial Fit (Smoothed)")
plt.grid()
plt.show()

# 输出拟合系数
print("Test1 三次拟合系数:", coef1_cubic)
print("Test2 三次拟合系数:", coef2_cubic)

test=[test1,test2]
#波长数据
x_need=[0.3,0.4,0.5,0.6,0.7]
y1_predict=poly1_cubic(x_need)
y2_predict=poly2_cubic(x_need)
y1_predict=y1_predict*np.mean(test_1)
y2_predict=y2_predict*np.mean(test_2)
#曲率数据
lamda0=[1529,1540]
c=4200
def lamda2K(y,i):
    return(c*(y-lamda0[i]))/lamda0[i-1]
y1_predict=lamda2K(y1_predict,0)
y2_predict=lamda2K(y2_predict,1)

def get_K(x,i):
    y_predict=poly1_cubic(x)/np.mean(test[i-1])
    y_predict=lamda2K(y_predict,i-1)
  

print(y1_predict)
print(y2_predict)

以上为第一问代码。其输出结果也一并贴在下方。

简谐振动的合成

两个同方向，同频率的简谐振动的合成

由于运动是同方向的，可以将位移的合成表达为代数加法，即

这个推导是纯数学的，让我们用几何的方法来理解一下，即使用旋转矢量方法来现场计算一下这个值（毕竟背这个公式有点……）

这样可以直接由几何关系，利用余弦定理求得A，再利用比值法求得

下面讨论两种特殊的情况：

1. 当两振动同相位（或可用诱导公式化为同相位）则：

   $$\text{if}\text{ }\phi_2-\phi_1=2k\pi,k\in N^+\\ \text{then }A=A_1+A_2$$
2. 当两振动反相位（或可用诱导公式化为反相位）则：

多个同方向、同频率简谐振动的合成：旋转矢量

用《普通物理学》的一道经典例题来讲解一下。

由几何关系容易得到，若选取第一个质点（这里假设为质点）运动方向为旋转参考系的x轴正向，则有：

两个同方向不同频率的简谐振动的合成 拍

两个同方向不同频率的简谐振动的和振动不再是简谐振动，下面先看一下它的一般表示

上式是一个相当复杂的运动，这里我们讨论一下：当

条件下，令

可以认为和运动近似为一个振幅为

的变振幅运动，这个振幅变化的频率称为拍频，即

谐振分析和频谱

傅里叶变换：

傅里叶变换的定义

对于一个连续时间函数 ，其傅里叶变换 定义为：

傅里叶逆变换

傅里叶逆变换（Inverse Fourier Transform）将频域信号 转换回时域信号 ：

离散傅里叶变换

对于离散时间信号 ( x[n] )，其离散傅里叶变换（Discrete Fourier Transform, DFT） ( X[k] ) 定义为：

其中，( N ) 是信号的长度，( k ) 是频率索引。

快速傅里叶变换

快速傅里叶变换（Fast Fourier Transform, FFT）是一种高效的算法，用于计算离散傅里叶变换。它利用了 DFT 的对称性和周期性，将计算复杂度从 ( O(N^2) ) 降低到 ( O(N · log N) )。

** 傅里叶变换的示例

假设我们有一个简单的时域信号

我们来计算它的傅里叶变换：

可以重点考虑一种特殊的情况：各个分运动都为某个基频整数倍的谐振合成。

两个相互垂直的，同频率简谐振动的合成

先说结论：轨迹是一个椭圆。下面来尝试证明一下。

这是一个椭圆的方程，由此方程可以得到，

1. $$\text{if }\Delta \phi=\phi_2-\phi_1=0\\y=\frac{A_2}{A_1}\cdot x$$

   这表示此时，振动退化成一条直线上的简谐运动，直线的斜率为y轴振幅与x轴振幅之比，如果以上述直线为x’轴建立运动方程，则：

   $$x'=\sqrt{A_1^2+A_2^2}\cos({\omega t+\phi})$$
2. $$\text{if }\Delta\phi=\pm \pi\\...$$
3. $$\text{if }\Delta\phi= \pi/2,\\\frac{x^2}{A_1^2}+\frac{y^2}{A_2^2}=1$$

两个相互垂直不同频率的简谐振动合成

阻尼振动 受迫振动 共振

阻尼振动

这里主要考虑一下阻力与速度成正比的情况，并且忽略所谓的辐射损失，推导阻尼振动的运动方程。设弹簧振子在线性阻力下运动，则：

什么是位带操作和位带区

位带操作

STM32内核的最小寻址单位是字节，一个字节里面有8位，所谓位带操作就是在STM32中实现位操作的方法。，我们先来看什么是位带区。

下面一张图片是Cortex-M内核寻址空间映射图。

图中的SRAM区里的0X20000000-0X200FFFF地址段和片内外设区里的0X40000000-0X400FFFFF地址段就是位带区，也就是设计支持位带操作的内存区域。在野火相关资料文档中，有这样一段解释：

那么，STM32是如何将内核寻址单位缩小到位的呢？位带区这两个1MB的空间除了可以像正常的RAM一样操作外， 他们还有自己的位带别名区，位带别名区把这1MB的空间的每一个位膨胀成一个32位的字，当访问位带别名区的这些字时，就可以达到访问位带区某个比特位的目的。

由此可以看出，想要对STM32实现位操作，只有随位带别名区的一个字空间（注意，不是字节空间）进行操作，而之所以不用字节则是因为这样会降低访问速度。

如何进行位带操作

我们可以通过指针的形式访问位带别名区地址从而达到操作位带区比特位的效果。

外设位带别名区地址

对于片上外设位带区的某一位空间，设其所在的字节地址为A，位序号为n（0<=n<=31），则该位对应的位带别名区地址为

0X42000000是外设位带别名区的起始地址，0x40000000是外设位带区的起始地址，（A-0x40000000）表示该比特前面有多少个字节， 一个字节有8位，所以*8，一个位膨胀后是4个字节，所以*4，n表示该比特在A地址的序号，因为一个位经过膨胀后是四个字节，所以也*4。

SRAM位带别名区地址

同样可以知道，

宏定义位带别名区地址的转换

#define BITBAND(addr,bitnum)((addr & 0xF0000000)+0x02000000+((addr &0x00FFFFF<<5)+(bitnum<<2))

好好理解一下这个公式！特别是其中按位与运算之巧妙！以下是野火开源资料对上述公示的描述。

addr & 0xF0000000是为了区别SRAM还是外设，实际效果就是取出4或者2，如果是外设，则取出的是4，+0X02000000之后就等于0X42000000， 0X42000000是外设别名区的起始地址。如果是SRAM，则取出的是2，+0X02000000之后就等于0X22000000，0X22000000是SRAM别名区的起始地址。

addr & 0x00FFFFFF 屏蔽了高三位，相当于减去0X20000000或者0X40000000，但是为什么是屏蔽高三位？因为外设的最高地址是：0X20100000， 跟起始地址0X20000000相减的时候，总是低5位才有效，所以干脆就把高三位屏蔽掉来达到减去起始地址的效果，具体屏蔽掉多少位跟最高地址有关。 SRAM同理分析即可。<<5相当于*8*4，<<2相当于*4，这两个我们在上面分析过。

下面介绍常用的宏定义

1
2
3

#define BITBAND(addr,bitnum)((addr & 0xF0000000)+0x02000000+((addr &0x00FFFFF<<5)+(bitnum<<2))
#define MEM_ADDR(addr)            *((volatile unsigned long *)addr)
#define BIT_ADDR(addr,bitnum)     MEM_ADDR(BITAND)(addr,bitnum)

上述宏定义中，BITAND用来将位带区某一位空间所在字节的首位地址和位偏移量映射为其在位带别名区的地址；MEM_ADDR用于将位带区某一位空间所在字节的首位地址转化为指针；

BIT_ADDR用于将位带区某一位空间所在字节的首位地址和位偏移量映射为对应的指针。（值得注意的是volatile关键字，需要提醒编译器每次存储或读取addr地址时重新从变量地址读取数据，避免优化）；由于地址是32位的，所以用无符号长整形表达地址。

GPIO的位带操作

我们来举一个例子：

如果我们要控制一个LED闪烁，利用库函数，我们需要经历一下算法：

1. 初始化GPIO引脚（低电平有效为例）
2. 控制GPIO为低电平，延时一段时间
3. 控制GPIO为高电平，延时一段时间
4. 回到2

然而利用位带操作，我们可以对单个管脚进行操作。当我们要操作一个位，直接用GPIO封装的宏直接访问这一位的数据。这样可以直接利用对应寄存器进行输出！上述算法变为：

1. 通过相应GPIO的寄存器地址的位带别名区地址，访问寄存器变量。可以利用宏定义：

   1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59

   // GPIO ODR 和 IDR 寄存器地址映射 #define GPIOA_ODR_Addr (GPIOA_BASE+20) #define GPIOB_ODR_Addr (GPIOB_BASE+20) #define GPIOC_ODR_Addr (GPIOC_BASE+20) #define GPIOD_ODR_Addr (GPIOD_BASE+20) #define GPIOE_ODR_Addr (GPIOE_BASE+20) #define GPIOF_ODR_Addr (GPIOF_BASE+20) #define GPIOG_ODR_Addr (GPIOG_BASE+20) #define GPIOH_ODR_Addr (GPIOH_BASE+20) #define GPIOI_ODR_Addr (GPIOI_BASE+20) #define GPIOJ_ODR_Addr (GPIOJ_BASE+20) #define GPIOK_ODR_Addr (GPIOK_BASE+20) #define GPIOA_IDR_Addr (GPIOA_BASE+16) #define GPIOB_IDR_Addr (GPIOB_BASE+16) #define GPIOC_IDR_Addr (GPIOC_BASE+16) #define GPIOD_IDR_Addr (GPIOD_BASE+16) #define GPIOE_IDR_Addr (GPIOE_BASE+16) #define GPIOF_IDR_Addr (GPIOF_BASE+16) #define GPIOG_IDR_Addr (GPIOG_BASE+16) #define GPIOH_IDR_Addr (GPIOH_BASE+16) #define GPIOI_IDR_Addr (GPIOI_BASE+16) #define GPIOJ_IDR_Addr (GPIOJ_BASE+16) #define GPIOK_IDR_Addr (GPIOK_BASE+16) // 单独操作 GPIO的某一个IO口，n(0,1,2...16),n表示具体是哪一个IO口 #define PAout(n) BIT_ADDR(GPIOA_ODR_Addr,n) //输出 #define PAin(n) BIT_ADDR(GPIOA_IDR_Addr,n) //输入 #define PBout(n) BIT_ADDR(GPIOB_ODR_Addr,n) //输出 #define PBin(n) BIT_ADDR(GPIOB_IDR_Addr,n) //输入 #define PCout(n) BIT_ADDR(GPIOC_ODR_Addr,n) //输出 #define PCin(n) BIT_ADDR(GPIOC_IDR_Addr,n) //输入 #define PDout(n) BIT_ADDR(GPIOD_ODR_Addr,n) //输出 #define PDin(n) BIT_ADDR(GPIOD_IDR_Addr,n) //输入 #define PEout(n) BIT_ADDR(GPIOE_ODR_Addr,n) //输出 #define PEin(n) BIT_ADDR(GPIOE_IDR_Addr,n) //输入 #define PFout(n) BIT_ADDR(GPIOF_ODR_Addr,n) //输出 #define PFin(n) BIT_ADDR(GPIOF_IDR_Addr,n) //输入 #define PGout(n) BIT_ADDR(GPIOG_ODR_Addr,n) //输出 #define PGin(n) BIT_ADDR(GPIOG_IDR_Addr,n) //输入 #define PHout(n) BIT_ADDR(GPIOH_ODR_Addr,n) //输出 #define PHin(n) BIT_ADDR(GPIOH_IDR_Addr,n) //输入 #define PIout(n) BIT_ADDR(GPIOI_ODR_Addr,n) //输出 #define PIin(n) BIT_ADDR(GPIOI_IDR_Addr,n) //输入 #define PJout(n) BIT_ADDR(GPIOJ_ODR_Addr,n) //输出 #define PJin(n) BIT_ADDR(GPIOJ_IDR_Addr,n) //输入 #define PKout(n) BIT_ADDR(GPIOK_ODR_Addr,n) //输出 #define PKin(n) BIT_ADDR(GPIOK_IDR_Addr,n) //输入

进行操作。（库函数中已经写好啦，现场查即可）

1. LED=0，延时；LED=1，延时；
2. 回到2；

注意：

1. STM32F7以上的MCU不支持位带操作。
2. out管脚作为左值使用，in管脚作为右值使用。

下面来写一下上述GPIO位带操作的实现举例。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

//.c文件核心代码
int main()
{
    //LED_Init
    LED_GPIO_Init();
    while(1){
      PFout(6)=0;
      SOFT_Delay(0x0FFFFF);
      PFout(6)=1;
      SOFT_Delay(0x0FFFFF);
    }
}
/*基于一般库函数的版本：
int main()
{
    RCC_HSE_Config(RCC_PLLSource_HSE_Div2,RCC_PLLMul_9);
    LED_Init();
    while(1)
    {
        GPIO_ResetBits(LED0_PORT,LED0_PIN);
        SOFT_Delay(0x0FFFFF);
        GPIO_ResetBits(LED0_PORT,LED0_PIN);
        SOFT_Delay(0x0FFFFF);
    }
}
*/

二叉树的特性：

1. 与一般树的根本区别：二叉树的每一个节点都恰好有两颗子树（其中一个或两个可以为空），而树的每一个元素可以有任意数量的子树。
2. 二叉树中，每个元素的子树是有序的，也就是说，有左子树和右子树之分。
3. 二叉树可以为空的。

4. 一颗有

   $$n>0$$

   个元素的二叉树有

   $$n-1$$

   条边，最大高度为$n$,最小高度为

   $$\left\lceil\log_2(n-1)\right\rceil$$

5. 一颗二叉树高度为h>=0，它至少有h个元素，最多有

   $$2^h-1$$

   个元素（称为满二叉树）

6. 完全二叉树是指对高度为h的满二叉树，从第一层到最后一层，在每层中从左至右顺序编号，删除k个编号为

   $$2^h-i(1≤i≤k<2^h)$$

   的元素得到的二叉树。然而，我们还有更为容易理解的一种定义：完全二叉树：深度为k的具有n个结点的二叉树，当且仅当其每一个结点都与深度为k的满二叉树中编号为1~n的结点一 一对应时，称之为完全二叉树。
   

7. 完全二叉树的特性：设完全二叉树的一元素其编号为i，1≤i≤n.则有

   1. 如果i=1，则该元素为二叉树的根；如果i>1,则其父节点的编号为

      $$i/2$$

   2. 有n个元素的完全二叉树，其高度为

      $$\left\lceil\log_2{(n+1)}\right\rceil$$
   3. 如果2i>n，则该元素无左孩，否则其左孩编号为2i

   4. 如果2i+1>n，则该元素无右孩，否则其右孩编号为2i+1.
      下面证明一下这个性质。
      当i=1，显然该元素为二叉树的根；当i>1时，考虑对应元素不在最下层，位于树的第

      $$\left\lfloor\log_2{i}\right\rfloor$$

      级上，其父节点位于

      $$\left\lfloor\log_2{i}\right\rfloor-1$$

      级上，且

      $$\frac{i-2^{\left\lfloor\log_2{i}\right\rfloor}}{2}=i_{parent}=\left\lfloor\frac{i}{2}\right\rfloor$$

      若2i>n，即

      $$i>\frac{n}{2}$$

      设高度为h,只需证：h-1层的最后一个元素的编号

   $$i_{previous} \geq n/2$$

   考虑最极端的情况，也就是满二叉树（我们当然可以知道满二叉树是一种特殊的二叉树），那么

   $$n=2^h-1$$

   ，而h-1层的最后一个元素的编号为

   $$i_{previous}=2^h{h-1}-1$$

   （注意这一点是与假设满二叉树无关的）
   显然满足上述条件。那么对于由满二叉树退化而来（注意这里的表述）的完全二叉树，我们可以知道，如果对应的满二叉树的元素数量为

   $$n_{max}>n$$

   ，则：

   $$i_{previous} \geq \frac{n_{max}}{2}>\frac{n}{2}$$

   故得证。同理可以完全对称地证明剩余的一个结论。

二叉树的描述：

1. 数组描述。
   二叉树的数组表示利用了性质7，把二叉树看作是缺少了部分元素的完全二叉树。将二叉树相对于完全二叉树（实际上，相对于满二叉树）缺少的部分也参与编号，对编号后的树建立数组，原有二叉树的元素按照其编号存储在数组的相应位置。一个有n个元素的二叉树最多需要

   $$2^n$$

   个空间来存储（包括了数组的零位置）。所以这是一种很浪费空间的描述方式。值得注意的是，在这种描述种我们用到了类似哈希表的思想，用空间换得了时间。比如，这样存储的二叉树，其查找的时间复杂度为O(1).

   1 2 3 4 5 6 7 8 9 10 11

   #define MaxSize 100struct TreeNode{ ElemType value;//结点中的数据元素 bool isEmpty;//结点是否为空} main(){ TreeNode t[MaxSize]; for (int i=0; i<MaxSize; i++){ t[i].isEmpty = true; } }

2. 链表描述。

   1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23

   #include<iostream> #include<queue> using namespace std; //binary search tree:left<=right struct bstNode { int data; bstNode* left; bstNode* right; }; //Creat a node bstNode* getNewNode(int data) { bstNode* newNode = new bstNode(); newNode->data = data; newNode->left = newNode->right = nullptr; return newNode; } template <class T> struct binaryTreeNode { T element; binaryTreeNode<T> *lChild,*rChild;

二叉树的常用操作

1. 二叉树的遍历
2. 求二叉树的高度
3. 复制二叉树
4. 插入节点
5. 删除节点
6. 查找元素
7. 求元素最值（int）
8. 判断是不是二叉搜索树
   下面是我写的主要操作的算法实现。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234

//Insertion
bstNode* Insert(bstNode* root, int data)
{
	if (root == nullptr)
	{
		root = getNewNode(data);
	}
	else if (data <= root->data)
	{
		root->left = Insert(root->left, data);
	}
	else if (data > root->data)
	{
		root->right = Insert(root->right, data);
	}
	return root;
}
//Search
bool Search(bstNode* root, int data)
{
	if (root == nullptr)return false;
	if (root->data == data)return true;
	else if (data < root->data)
	{
		return Search(root->left, data);
	}
	else if (data > root->data)
	{
		return Search(root->right, data);
	}
}
//Find Min and Max
int findMin(bstNode* root)
{
	if (root == nullptr)
	{
		cout << "Error:empty tree" << endl;
		return  -1;
	}

	bstNode* current = root;

	while (current->left)
	{
		current = current->left;
	}

	return current->data;
}
int findMax(bstNode* root)
{
	if (root == nullptr)
	{
	cout << "Error:empty tree" << endl;
	return -1;
	}
	bstNode* current = root;
	while (current->right)
	{
		current = current->right;
	}
	return current->data;
}

//FindMax using recursion
int recursMax(bstNode* root)
{
	bstNode* current = root;
	if (current->right == nullptr)
	{
		return current->data;
	}
	else return recursMax(current->right);
}

//Height of tree 
//is the number of edges in longest path 
//from root to leaf node
//Get Height(recursion)
int Height(bstNode* root)
{
	if (root == nullptr)return -1;
	return 1 + (Height(root->left) >= Height(root->right) ? Height(root->left) : Height(root->right));
}

//Traversal
//process of visiting each node in the tree exactly once in some order
//
//Breadth-first
//Using queue:(LIFO)
//Inserting all the children of current node into a queue 
//Visiting the data of the current node
//
void LevelOrder(bstNode* root)
{
	if (root == nullptr) return;
	queue<bstNode*>Q;
	Q.push(root);
	//while the queue is not empty
	while (!Q.empty())
	{
		bstNode* current = Q.front();
		cout << current->data << " ";
		if (current->left)Q.push(current->left);
		if (current->right)Q.push(current->right);
		Q.pop();
	}
	cout << endl;
}
//Time:O(n)
//Space:Avg->O(n)
//Depth_first
//1.root->left->right(Preorder)
void Preorder(bstNode* root)
{
	cout << root->data<<" ";
	if (root->left)
	{
		Preorder(root->left);
	}
	if (root->right)
	{
		Preorder(root->right);
	}
}
//2.left->root->right(Inorder)
void Inorder(bstNode* root)
{
	if (root == nullptr) return; // 如果当前节点为空，直接返回

	Inorder(root->left);         // 递归访问左子树
	cout << root->data << " ";   // 访问当前节点
	Inorder(root->right);        // 递归访问右子树
}
//3.left->right->root(Postorder) 
void Postorder(bstNode* root)
{
	if (root == nullptr)return;
	Postorder(root->left);
	Postorder(root->right);
	cout << root->data << " ";
}
//using recursion
//bool isSubtreeLesser(bstNode* root,int val)
//{
//	if (root == nullptr)return true;
//	if (root->data <= val
//		&& isSubtreeLesser(root->left, val)
//		&& isSubtreeLesser(root->right, val))return true;
//	else return false;
//}
//bool isSubtreeGreater(bstNode* root, int val)
//{
//	if (root == nullptr)return true;
//	if (root->data > val
//		&& isSubtreeGreater(root->left, val)
//		&& isSubtreeGreater(root->right, val))return true;
//	else return false;
//}
//bool isBst(bstNode *root)
//{
//	if (root == nullptr)return true;
//	if (isSubtreeLesser(root->left, root->data)
//		&& isSubtreeGreater(root->right, root->data)
//		&& isBst(root->left)
//		&& isBst(root->right)
//		)return true;
//	else return false;
//}
//better edition
bool isBst(bstNode* root, int minVal= INT_MIN, int maxVal=INT_MAX)
{
	if (!root)return true;
	if (isBst(root->left, minVal, root->data)
		&& isBst(root->right, root->data, maxVal)
		&& root->data<maxVal && root->data>minVal)return true;
	else return false;
}
//Delete a node from bst
bstNode* Delete(bstNode* root, int data)
{
	if (!root)return root;
	else if (data < root->data)root->left = Delete(root->left, data);
	else if (data > root->data)root->right = Delete(root->right, data);
	else//found
	{
		//no child
		if (root->left == nullptr && root->right == nullptr)
		{
			delete root;
			root = nullptr;
			return root;
		}
		//one child
		else if (root->left == nullptr)
		{
			bstNode* tmp = root;
			root = root->right;
			delete tmp;
			return root;
		}
		else if (root->right == nullptr)
		{
			bstNode* tmp = root;
			root = root->left;
			delete tmp;
			return root;
		}
		//two children
		else 
		{
			bstNode* tmp = FindMin(root->right);
			root->data = tmp->data;
			root->right = Delete(root->right, tmp->data);
		}


	}
}
bstNode* FindMin(bstNode* root)
{
	if (root == nullptr)
	{
		cout << "Error:empty tree" << endl;
		return nullptr;
	}
	bstNode* current = root;
	while (current->right)
	{
		current = current->right;
	}
	return current;
}

在进行二叉树遍历的时候，有这样四种遍历方式：

1. 前序遍历（PreOrder）:root->left->right
2. 中序遍历（InOrder）:left->root->right
3. 后序遍历（PostOrder）:left->right->root
4. 层次遍历（LevelOrder）

对于前三种，他们的递归形式很好理解，以前序遍历为例，其算法可以表述为：

1. 访问当前节点。
2. 如果左孩不为空，前序遍历左子树。
3. 如果右孩不为空，前序遍历右子树。

我们来看看如何把它写成迭代的形式。

这里以前序遍历为例。迭代形式的算法可以表述为：

1. 建立一个栈空间Q
2. 当我们遍历到当前节点current时，读取这个节点的数据
3. 如果当前节点的左孩不为空，就把当前节点压入Q，将当前节点移到左孩处
4. 如果当前节点的左孩为空，将Q的栈顶弹出，当前节点回到其父节点。
   a. 此时，如果当前节点有右孩，就把当前节点移到右孩，重复2~4.
   b. 如果此时当前节点没有右孩，则重复4.

基于这种迭代方法，我们可以显示地将递归形式中通过函数调用的栈空间用Q栈表示出来了。以下为具体的实现代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        if (!root) return {};  // 如果根节点为空，直接返回空结果
        stack<TreeNode*> S;
        vector<int> v;
        TreeNode* rt = root;

        while (rt || !S.empty()) {
            while (rt) {
                v.push_back(rt->val);  // 访问当前节点
                S.push(rt);            // 将当前节点压入栈
                rt = rt->left;         // 转向左子树
            }

            if (!S.empty()) {
                rt = S.top();  // 弹出栈顶节点
                S.pop();
                rt = rt->right;  // 转向右子树
            }

值得注意的是，此时虽然我们用了递归方法，但这种方法的时间复杂度并不一定低于迭代方法。

二叉树的层序遍历则是使用了队列的数据结构，其算法过程描述如下：

1. 建立一个队列Q。
2. 将根节点入Q列。
3. 如果Q列不为空，则从队头弹出一个节点，读取其数据并将其孩子节点（如果存在）入列。
4. 重复3，直到Q列空，返回。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

void LevelOrder(bstNode* root)
{
if (root == nullptr) return;
queue<bstNode*>Q;
Q.push(root);
//while the queue is not empty
while (!Q.empty())
{
bstNode* current = Q.front();
cout << current->data << " ";
if (current->left)Q.push(current->left);
if (current->right)Q.push(current->right);
Q.pop();
}
cout << endl;
}

应用举例：信号放大器问题

基础理论

图，有向图，无向图的定义这里从略。

定义1 无环，无重边的图称为简单图。

定义2 任意两顶点均相邻的简单图称为完全图。含有n个顶点的完全图记为$K_n$

定义3 顶点的度：

（1）在无向图中，与顶点v关联的边的数目（环算两次）称为这个点的度，记为$d（v）$

（2）在有向图中，从顶点v引出的弧的数目称为v的v的出度，记为$d^+(v)$,从该点引入的弧的数目称为入度，记为$d^-(v)$,两者相加之和记为顶点的度。

定理1 对任意图，有

推论：任何图中的奇顶点总数为偶数.

图的矩阵表示

1.关联矩阵
对于无向图 ${G}$，其关联矩阵 ${M=(m_{ij}){n\times m}}$，其中

对于无向图${G}$其关联矩阵 ${M=(m_{ij}){n\times m}}$，其中

2.邻接矩阵

对于无向赋权图 ${G}$，其邻接矩阵 ${W=(m_{ij}){n\times m}}$，其中

对于有向赋权图，上式改为：

最短路算法

1.Dijkstra算法（贪心算法）
这是一种贪心算法，其主要用到的是迭代方法。它的依据是一个重要且明显的性质：最短路是一条路，它的任意子路也是该子路两端点间的最短路。
该算法的核心思想是：从起点由近及远地求得到各点的最短路和距离，直到到达某个顶点。
为了避免重复并保留每一步的计算信息，对于任意顶点$v_i$定义两个记号：

算法的操作可以这样表示：

令起点$u_0$：

其中，$w_{uv}$表示顶点u和v之间边的权值.如果利用上一个节点对当前节点的$l(v)$进行了修改，则$z(v)=v_{previous}$
,否则$z(v)$不变.
计算$min\{l(v)\}$,把达到这个最小值的一个顶点即为$u_{i+1}$,令$S_{i+1}=S_i$
算法用伪代码表示如下：
Q = G.V // Q 是一个优先队列，按 $l(v)$排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

// 主循环
DIJKSTRA(G, w, s)
// 初始化
for each vertex v in G.V:
l(v) = ∞
z(v) = NIL
l(s) = 0
S_i =
while Q is not empty:
    u = EXTRACT-MIN(Q)  // 从 Q 中取出 l(v) 最小的顶点 u
    S_i = S_i ∪ {u}    // 将 u 加入永久标号集合 S_i
    for each vertex v in G.Adj[u]:  // 遍历 u 的所有邻接顶点 v
        if l(v) > l(u) + w(u, v):  // 松弛操作
            l(v) = l(u) + w(u, v)
            z(v) = u
            DECREASE-KEY(Q, v, l(v))  // 更新 Q 中 v 的优先级

下面是用python实现的算法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

import heapq

def dijkstra(graph, start):
    # 初始化距离字典和父顶点字典
    l = {vertex: float('inf') for vertex in graph}
    z = {vertex: None for vertex in graph}
    l[start] = 0  # 起点的距离为0

    # 使用优先队列存储 (距离, 顶点) 对
    priority_queue = [(0, start)]

    while priority_queue:
        current_distance, u = heapq.heappop(priority_queue)

        # 如果当前距离大于已知最短距离，则跳过
        if current_distance > l[u]:
            continue

        # 遍历邻接顶点
        for v, weight in graph[u].items():
            distance = current_distance + weight

            # 如果发现更短路径，则更新
            if distance < l[v]:
                l[v] = distance
                z[v] = u
                heapq.heappush(priority_queue, (distance, v))

    return l, z

# 示例图的邻接表表示
graph = {
    'A': {'B': 1, 'C': 4},
    'B': {'A': 1, 'C': 2, 'D': 5},
    'C': {'A': 4, 'B': 2, 'D': 1},
    'D': {'B': 5, 'C': 1}
}

l, z = dijkstra(graph, 'A')
print("最短距离:", l)
print("父顶点记录:", z)

2.Floid算法：（动态规划）

如果一个节点位于起点到重点的最短距离路径上，以节点0→8为例，

1. $$l（0→8）=l(0 \to 4)+l(4\to 8)(\text{if 4} \in \text{the shortest way }) \\ l（0→8）<l(0 \to 6)+l(6\to 8)(\text{if 6} \notin \text{the shortest way })$$
2. Python代码（片段）：

1
2
3
4
5
6

for k in range(self.V):
	for i in range(self.V):
		for j in range(self.V):
			if self.D[i][k]+self[k][j]<self.D[i][j]:
				self.D[i][j]=self.D[i][k]+self[k][j]
				self.S[i][j]=self.S[i][k]

算法（2）排序算法

1、插入排序

1.1 直接插入排序：

直接插入排序的基本思想：

1）将整个数组分为“已排序”和“未排序”的两部分，设已排序m，总长度n

2）从未排序部分选取第一个元素

3）遍历已排序的数组，查找需要插入的位置下标i

4）保护待排序数据，将下标大于i，小于m的所有元素右移一位

5）插入，进入下一轮循环

1
2
3
4
5
6
7
8
9
10
11
12
13
14

void InsertSort(type* arr, int num)
{
	for (int m = 1; m < num; m++)//外层for循环，用于记录已经排序好的长度m
	{
		type tmp = arr[m];
		int i = m - 1;
		for ( i = m - 1; i >= 0&&arr[i]>tmp; i--)//内层for循环，用于遍历已排序的数组
		{
			arr[i + 1] = arr[i];
		}
		arr[i+1] = tmp;
	}
}

算法的性能分析：

时间复杂度：O（n^2）

（平均情况下向长度为m的序列中插入一个数据的平均移动速度是m/2，m从1累加到n-1）

空间复杂度：O（1）

稳定性：稳定

2、交换排序

2.1 快速排序

1）递归调用自身

2）每次将数组以“主元”为界分为较大组和较小组，再对两组分别进行快速排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

#include <algorithm> // 用于 std::swap

int Partition(int* arr, int num, int nLower, int nUpper) {
	int pivot = arr[nLower]; // 选取第一个元素作为主元进行切割
	int nLeft = nLower + 1;
	int nRight = nUpper; // 确定本次分割的范围

	while (true) {
		while (nLeft <= nRight && arr[nLeft] <= pivot) nLeft++; // 查找左侧第一个大于 pivot 的元素对应的下标
		while (nRight >= nLeft && arr[nRight] >= pivot) nRight--; // 查找右侧第一个小于 pivot 的元素对应的下标
		if (nLeft > nRight) break; // 循环退出条件
		if (nLeft < nRight) { // 如果左标小于右标，交换找到的两个下标对应的数的位置
			std::swap(arr[nLeft], arr[nRight]);
		}
	}
	std::swap(arr[nLower], arr[nRight]); // 将主元放到正确的位置
	return nRight; // 返回主元的最终位置
}

void QuickSort(int* arr, int num, int nLower = 0, int nUpper = -1) {
	if (nUpper == -1) nUpper = num - 1; // 缺省参数的情况，nUpper 应该是 num - 1
	if (nLower < nUpper) {
		int nSplit = Partition(arr, num, nLower, nUpper); // 划分数组
		QuickSort(arr, num, nLower, nSplit - 1); // 递归排序左侧子数组
		QuickSort(arr, num, nSplit + 1, nUpper); // 递归排序右侧子数组
	}
}

算法性能分析：

快速排序在n较大时时间复杂度O（nlogn）

在n较小时或主元选择不合理时，时间复杂度为O（n^2）

空间复杂度O（logn）

快速排序是不稳定的

3、选择排序

3.1直接选择排序

1）数组被分为已排序与未排序两组

2）每次遍历未排序组找到最小的元素插入已排序组的最后

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

template <typename type>
void selectSort(type* items, int len)
{
	for (int i = 1; i < len; i++)
	{
		int imin = i - 1;
		for (int j = i; j < len; j++)//j从i开始，在i后寻找最小的排到已经排序的前序列后一个
		{
			if (items[j] < items[imin]) {
				imin = j;
			}
		}
		if (imin != i - 1)//如果找到了，将最小值放置到i-1处
		{
			type t = items[i - 1];
			items[i - 1] = items[imin];
			items[imin] = t;
		}
	}
}

欢迎来到我的博客。

这是我用Hexo+Github搭建的第一个博客。我将在这里分享我的学习笔记，日常感慨和读书笔记等。

本站关键词:
技术 理论 生活